Esta trilha é chamada de Trilha Euleriana
 |
Portanto G é um Grafo Euleriano.
 |
Tomemos um grafo euleriano G.
Seja T uma trilha euleriana de G com origem em u.
Seja v um vértice qualquer de T
Caso 1: v ![]() u { Todos os vértices internos da trilha
tem grau par }
u { Todos os vértices internos da trilha
tem grau par }
Provemos por Indução no número de arestas (m).
Base : (m=0)
Portanto, existe uma trilha euleriana em G, que pode ser encontrada aplicando-se o seguinte algoritmo:
Representação do Problema usando Teoria dos Grafos:
Seja G um grafo onde
VG = { 0 , 1 , 2 , 3 , 4 , 5 , 6 } // Números que aparecem nas
pedras do dominó.
AG = { (0,0) , (0,1) , ... , (0,6) , (1,1) , (1,2) , ... , (1,6) ,
(2,2) , ... , (6,6) } // Peças do dominó.
Problema: G é Euleriano ?
Resposta: O Grafo G é um grafo completo, com 7 vértices,
acrescido de um laço em cada vértice, e portanto, todos os
vértices de G tem grau 8 ( Par ). Logo, pelo teorema
1, G é Euleriano.
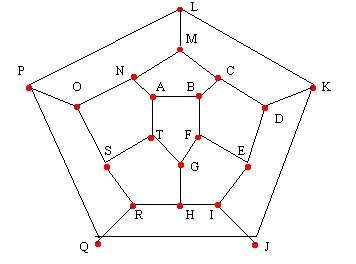 |
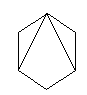
| O Dodecaedro é Hamiltoniano pois existe um ciclo que
passa por todos os vértices (Lembre-se que num ciclo apenas o primeiro vértice se repete) |
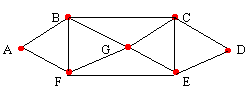
Exemplos:
 |
 |
 |
 |
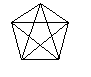
n=5 (vértices)
2 + 5 2 + 4 1 + 3 É hamiltoniano |
Note que o grafo acima não satisfaz a condição de Dirac.
Exercício: Provar que a condição de Ore engloba a condição de Dirac ( A condição de Dirac é uma consequência da condição de Ore)
 |
 |
 |
 |
 |
 |
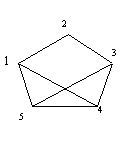
O Grafo abaixo não satisfaz as condições de Bondy e Chvata, Ore, Dirack, mas é um grafo hamiltoniano, porque
possui um ciclo hamiltoniano
Grafo G Fecho de G Considerações:
Embora todas estas considerações não podemos afirmar que o grafo não é hamiltoniano, porque não satisfaz nenhuma destas condições.
- Pela condição de Dirac, ele seria hamiltoniano se Gr(v)
n/2, com n
3, o exemplo acima não satisfaz esta condicao, visto que n=6, o grau dos vértices teria de ser
3, o que não acontece no exemplo acima pois todos os vértices possuem grau 2
- Pela condição de Ore, a soma dos graus de vértices não adjacentes deveria ser
número de vértices, o que não acontece no exemplo acima, todos os pares de vértices não adjacentes possuem a soma de seus graus igual a 4, e o grafo possui 6 vértices, o que não respeita a condição
- Pela condição de Bondy e Chvata o fecho do grafo teria de ser um grafo completo, o que não acontece no grafo acima.
O grafo é hamiltoniano, pois possui um ciclo hamiltoniano
Exercício: Provar que um Grafo completo é hamiltoniano
Como em um grafo completo todos os vértices estão ligados entre si é possível, partindo de um vértice inicial v0 eu passar por todos os vértices e voltar ao vértice inicial v0, sem que haja repetição de vértices encontrando assim um ciclo hamiltoniano, e portanto o grafo é hamiltoniano.