Todo grafo acíclico é simples.
Um grafo acíclico e conexo é uma árvore
Um grafo acíclico é chamado também de Floresta ( Cada componente conexo é uma árvore ) .
 |
 |
 |
|
|
|
|
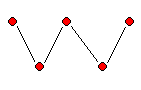
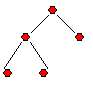
Onde G1, G2,G3 são árvores
G1+G2+G3 é uma floresta.
Grafo Acíclico é um grafo que não contém ciclos.
Todo grafo acíclico é simples.
Um grafo acíclico e conexo é uma árvore
Um grafo acíclico é chamado também de Floresta ( Cada componente conexo é uma árvore ) .
G1 G2 G3 Onde G1, G2,G3 são árvores
G1+G2+G3 é uma floresta.
Suponhamos que existam 2 caminhos distintos P e Q ligando dois vértices x,y
VG.
Logo, existe uma aresta= (u,v)
AG tal que
P e
Q ( sem perda de generalidade ) .
PQ é um subgrafo conexo de G, logo, em PQ -existe um passeio de u a v.
Então, por um teorema anterior ,um caminho R de u a v em PQ -
.
Portanto, Ré um ciclo em G.
Absurdo, visto que G é árvore.
Por indução em n {Ordenado por numeros de Vértices)
Base: ( n = 1 )|AG| = 0 = n - 1Hípotese de InduçãoSe G é uma árvore com k < n vértices, então G possui k-1 arestas.Passo: ( n >1 ){Assumir que é verdade para todas as árvores com mais que 1 árvore}Seja G uma árvore com n vértices.
Tome uma aresta (u,v)AG e considere os componentes distintos K1 e K2 obtidos pela retirada de (u,v) de AG, de forma que u
K1 e v
K2 . {Quando eu retiro a aresta u e v eu tenho K1 e K2 que são componentes conexas,Problema:Provar que quando eu retiro a aresta eu realmente tenho uma componente conexa}
Árvore com n vértices K1 K2 Como |VK1| < n e |VK2| < n, temos pela Hipótese de Indução que:
|AK1| = |VK1| - 1 e |AK2| = |VK2| - 1{O numero de arestas é igual ao numero de vértices -1}.Agora, |AG| = |AK1| + |AK2| + 1,
Logo |AG| = |VK1| -1 + |VK2| - 1 + 1
E portanto,|AG| = |VK1| + |VK2| - 1 = n -1.
Portanto:
Comogr(v) = 2 |AG| e,{Teorema da Soma dos Graus}
pelo teorema anterior, |AG| = n -1Temos que
2(n-1)2(n-1) +1 {A soma dos graus do vertice de uma Arvore = 2(narestas-1)
2n -22n -1
- 2- 1
12 Absurdo!!!