Raciocínio com Incerteza

---

Raciocínio Probabilístico

Revisão de Probabilidade

Axiomas:
1.  0 <= P(A) <= 1
2.  P(True) = 1    P(False) = 0
3.  P(A v B) = P(A) + P(B) - P(A ^ B)

Probabilidade Condicional e Regras Auxiliares:
1.  P(A|B) = P(A ^ B) /  P(B)
2.  P(A ^ B) = P(A|B).P(B)

Regra de Bayes:

                        P(A|B).P(B)
1.  P(B|A) =   ------------------
                            P(A)

Aplicação da Regra de Bayes

P(D | M) = 0.5      /* Em 50% dos casos, a meningite provoca dores no pescoço */
P(M) = 1/50000    /* Uma pessoa, em cada 50000, possui meningite */
P(D)  =  1/20         /*  Uma pessoa, em cada 20, tem dores no pescoço */

P(M | D ) = ?  /* Quais as chances de que uma paciente que tenha reclamado de dor no pescoço esteja com meningite */

P(M | D ) = P ( D | M ). P (M) /  P(D)  =   (0.5 X  1/50000 ) /  (1/20) =  0.0002

Redes Bayesianas

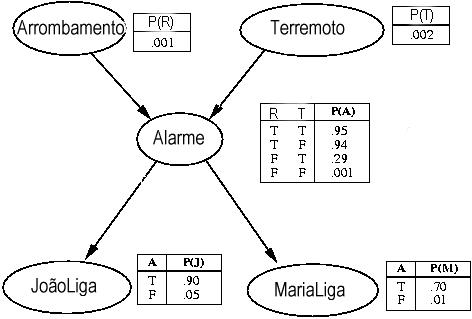
A rede bayesiana  representa a seguinte situação: você tem um alarme anti-arrombamento instalado em casa. Ele é bastante confiável na detecção de arrombamento, mas as vezes ele dispara quando acontecem pequenos tremores de terra. Você tem dois visinhos, João e Maria, que prometeram ligar no seu trabalho caso ouçam o alarme tocar. João sempre liga quando ouve o alarme, mas as vezes ele confunde o som do telefone com o alarme, e liga. Maria, por outro lado, gosta de ouvir musica alta, e as vezes não ouve o alarme tocar.

Algumas Informações representadas na redes bayesiana:

- A probabilidade a priori de acontecer um arrombamento, P(R), é 0,1%, enquanto a de acontecer um terremoto P(T), é 0,2% [Terremotos, na cidade em questão, são mais freqüentes que arrombamentos]
- A probabilidade do alarme tocar sem ter acontecido arrombamento ou terremoto é de 0,1% [O alarme pode disparar por alguma falha técnica, por exemplo]
- P[A|R] = 94% e P[A|T] = 29%. [O Alarme é mais sensivel a arrombamento que terremotos]

Exemplo de pergunta que pode ser respondida utilizando técnicas de inferência em redes Bayesianas: qual a probabilidade de que o alarme toque mesmo não tendo acontecido nem arrombamento, nem terremoto, e mesmo sabendo que tanto João quanto Maria ligaram ?

P(J^M^A^~R^~T) = P(J|A)   X    P(M|A)  X   P(A|~R^~T)    X   P(~R)   X    P(~T) =
                                    0.90     X       0.70    X            0.001       X   0.999   X    0.998  =  0.00062

Lógicas Não Monotônicas

Exemplos

José está indo visitar Maria e no caminho passa por uma floricultura.
Para decidir se deve ou não levar flores para Maria ele usa as seguinte informações.
• Devemos, quando possível, dar as pessoas o que elas gostam. [ gosta(x,y) -> levar(x,y) ]
• Mulheres gostam de flores. [  mulher(x) -> gosta(x,flores) ]
• Maria é mulher. [ mulher(maria) ]
• Teorema: devo levar flores para Maria. [ levar(maria,flores) ]

Chegando na casa de Maria, José é surpreendido com um ataque de alergia à flores, de Maria.
Neste momento sua base de conhecimentos deve ser revista.
E o ''teorema'' recém provado passa a ser falso.
Novo conhecimento:
~gosta(maria,flores). /* Supomos também que alergia(x,y) -> ~gosta(x,y) */

Raciocínio por Omissão (Reiter)

Permite regras do tipo:
1) Se X não for conhecido, então concluir Y.  (Nem tudo é armazenado explicitamente na base de dados).
2) Se X não puder ser provado, então concluir Y. 
3) Se X não puder ser provado em um tempo pré-definido, então concluir Y.

• Provas dependem de informação não relacionada com o domínio.
• Poder computacional influi no resultado.
• Difícil caracterizar formalmente o processo de prova.

Exemplo: A menos que seja possível provar que uma determinada mulher não "gosta" de flores, assuma que todas as mulheres gostam de flores [mulher(x) -> gosta(x,flores) - A menos que ~gosta(x,flores) . ]

Informações Complementares

• Página da UFSC sobre Representação de Incerteza
• Links para Material Relacionado com Redes Bayesianas
• Mycin - Fatores de Incerteza