Espaço de Estados
Links Interessantes
Prof. J. J. Alferes - Univ. Nova de Lisboa Exemplos de problemas clássicos que podem ser modelados por espaços de estados
Prof. Ralph Morelli - Trinity College Notas de aula sobre espaço de estados com revisão de teoria dos grafos
Prof. Roland Bol - Uppsala Universitet Exemplos de problemas modelados por espaços de estados
Exemplos de Espaços de Estados
| Conceitos |
Exemplo |
| Problema |
Problema das 8 peças (8-puzzle) |
Espaço de Estados do
Problema
(Configurações Relevantes) |
...
...
.. |
| Estados Iniciais |
|
Estados Meta (ou Alvo)
|
|
Operadores (Regras que permitem
mudança de estado) |
"Mover espaço" para cima, para
baixo, para a esquerda ou para a
direita. |
Representação de Operadores:
I - Se ( (B 1 2) (3 5 4) (6 8 7) ) então (
(1 B 2) (3 5 4) (6 8 7) )
II - Se Espaço em Linha X, Coluna Y então
Mova espaço
para Linha W, Coluna Z
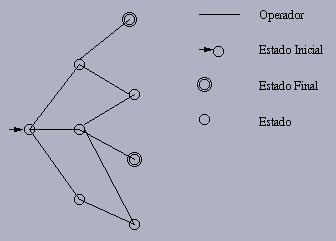
Representação Gráfica de um Espaço de
Estados
Exemplo 2: Problema do Vasilhame (Livro da Elaine Rich)
Problema do Vasilhame: Dado um vasilhame de 4 e outro de 3 litros, sem
marcação,
colocar exatamente 2 litros de água dentro do vasilhame de 4
litros.
Há
uma bomba que pode ser usada para colocar água nos vasilhames,
inicialmente vazios.
Espaço de Estados: (0,0) (1,0) (1,0) (2,3) (4,3)
...
Estado Inicial: (0.0)
Estado Final: (2,n)
Operadores:
1. Se (x,y) e x < 4 entao
(4,y)
; Encher v4
2. Se (x,y) e y < 3 entao
(x,3)
; Encher v3
3. Se (x,y) e x > 0 entao
(0,y)
; Esvaziar v4
4. Se (x,y) e y > 0 entao
(y,0)
; Esvaziar v3
5. Se (x,y) e x+y >= 4 e y>0 entao (4,y-(4-x)) ;
Encher v4 usando v3
6. Se (x,y) e x+y >= 4 e x>0 entao (x-(3-y),3) ;
Encher v3 usando v4
7. Se (x,y) e x+y < 4 e y>0 entao
(x+y,0) ;
Despejar
v3 em v4
8. Se (x,y) e x+y < 3 e x>0 entao
(0,x+y) ; Despejar v4 em v3
Algumas Suposições Implícitas na
Descrição:
Podemos despejar água no chão
Podemos despejar água de um vasilhame em outro
Solução: 2 , 7 , 2 , 5 , 3 e 7
Exemplo 3 - Jogar Xadrez
| Conceitos |
Exemplo |
|
Jogar, e se possível ganhar, uma partida de xadrez |
| Espaço de Estados - Configurações
Relevantes |
Situações possíveis para o tabuleiro |
| Estados Iniciais |
Situação inicial do tabuleiro |
| Estados Meta |
Situações do tabuleiro em que o computador
ganha |
| Operadores |
Regras para movimentação de peças |
Avaliar as seguintes opções para
representação de operadores:
I - Se "Matriz representando estado do tabuleiro"
então "Matriz com uma peça alterada"
II - Se "Peão Branco em (X,Y) e (Z,W)
está livre" então "Mova de (X,Y) para (Z,W)
Outros Exemplos
4. Missionários e Canibais: Transportar, de uma margem
à outra de um rio, um grupo de 3 missionários e 3
canibais, de
forma que, em nenhum
momento, o número de canibais seja maior que o número de
missionários.
Existe um único barco que pode ser usado para transportar no
máximo
dois passageiros.
Espaço de Estado: (C M B)
C - Total de Canibais na Margem Esquerda (3-C =
Total
de Canibais na Margem Direita)
M - Total de Missionarios na Margem Esquerda (3-M =
Total
de Canibais na Margem Direita
B - 1 = Barco na Margem Esquerda, 0 = Barco na
Margem Direita
Restricoes: 0 <= C,M <= 3
M >= C
0 <= B <=
1
Estado Inicial: (3 3 1) // 3 Canibais, 3 Missionários e 1
barco
na
margem esquerda.
Estado Meta: (0 0 0) // 0 Canibais, 0 Missionários e
1
barco
na margem direita.
Operadores: Movimentam canibais e missionários de um lado ao
outro do
rio.
Clique aqui
para acessar um applet que ilustra o problema.
5. Cubo Mágico: Encontrar um sequência de
passos para resolver o cubo mágico a partir de qualquer
configuração inicial.
6. Problema do Dominó: Formar um círculo com
todas as peças do domínio, sem desobedecer as regras de
"encaixe" do jogo.
7. 8-Rainhas: Distribuir 8 rainhas em um tabuleiro de
xadrez de forma que nenhuma esteja sendo atacada (mesma linha, coluna
ou diagonal).
Importante: Note que o caminho da
busca não tem importância para os problemas 6 e 7.
8. Criptoaritmética: (Encontrar
substituições de
letras por números respeitando as regras da aritmética)
SEND
+ MORE
------
MONEY |
FIVE
FIVE
+ NINE
ELEVEN
------
THIRTY |
DOS
+ DOS
TRES
-----
SIETE |
9. Resta-1: Criar um simulador para o conhecido jogo
resta-1.
10. Coloração: Colorir um mapa utilizando no
máximo n-cores (n é determinado pelo
usuário). Ver disciplina Teoria dos Grafos para
informações de como modelar esse problema.
