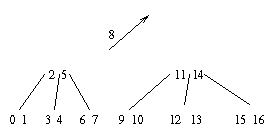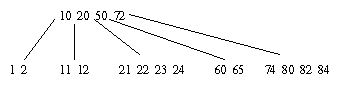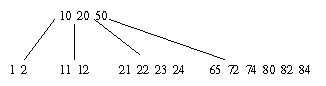Árvores B (B-Trees)

Motivação

Usada quando parte das chaves devem ser armazenadas num dispositivo de armazenamento secundário de acesso em blocos (ou setores) (E.g. Disco Rígido).

Cada nó da árvore deve ocupar exatamente um bloco (setor) do dispositivo secundário. (E.g.: 512 bytes)

Nós podem conter um número variável de chaves.

Seja d um número inteiro >= 2.
Um árvore B de ordem d possui as seguintes propriedades:

1. Todo nó tem no mínimo d e no máximo 2d chaves. (Com exceção da raiz que tem de 0 a 2d chaves)
2. Nós não folha, com x chaves, tem exatamente x+1 filhos. (Em cada nó, ponteiros e chaves se intercalam, numa sequência que começa e termina com um ponteiro. Cada chave, de nó não folha, possui um filho direito e um filho esquerdo)
3. Dada uma chave c temos que: chaves à esquerda de c (tanto dentro do nó quanto no filho esquerdo) devem ser menores que c e chaves à direita de c devem ser maiores que c. (Propriedade análoga àquela que define uma ABB).
4. Todas as folhas devem estar num mesmo nível.

Cálculo da Ordem da Árvore

P = Tamanho de cada ponteiro (Ex: 4 bytes)
C = Tamanho de cada chave (Ex: 2 bytes)
S = Tamanho de um setor de disco (Ex: 512 bytes)
D = Ordem Procurada

Tc = Total máximo ocupado pelas chaves
Tp = Total máximo ocupado pelos ponteiros
Tg = Total máximo de ocupação de um nó

Tc = 2*D*C  // No máximo teremos 2D chaves em um nó.
Tp = (2*D+1)*P
Tg = Tc + Tp
Tg < S => Tc + Tp < S
2*D*C + (2*D+1)*P < S
2*D*C + 2*D*P + P < S
D*(2*C +2*P) + P < S
D <  (S-P) / 2*(C+P)      (Menor ou igual, para ser mais preciso)
D = Piso( (S-P) / 2*(C+P) )

No exemplo,
D = Piso ( (512-4)/2*(2+4) ) = Piso( 42.33 ) = 42

Busca

Análoga a busca em ABB.
A busca por uma chave dentro de um nó pode ser feita através de uma busca binária, uma vez que as chaves ficam ordenadas dentro de cada nó.

Inserção

1. Buscar nó folha em que deve ser inserida a nova chave.
2. Inserir a chave mantendo a ordenação (sem se preocupar em ultrapassar o limite 2d)
3. Seja t o total de chaves do nó que sofre a inserção
4. Se t > 2d
5.     Efetuar Cisão
6.     Propagar teste para o pai (linha 3 em diante)
7. Senão
8.     Fim.

Cisão: Transferir a chave central para o pai e dividir o nó em dois.
 

	Árvore Inicial (Ordem 2)
	Inserção da Chave 4
	Cisão do nó (0 1 2 3 '4' ) Chave 2 passa para o pai. Pai passa a ter 5 chaves.
	Cisão do nó ('2' 5 8 11 14 ) Chave 8 passa para o pai ...

Definições Auxiliares

Página: Nó de uma B-Árvore.
Irmãos Adjacentes: Mesmo pai e ponteiros adjacentes no pai.
ch(N): Total de chaves da página N

Remoção

Buscar chave r a ser removida. (Seja R o nó com a chave r)
Se R é folha
     Remova r de R
Senão
    Troque r pelo sucessor. (Certamente está numa folha).
     Seja r a nova chave e R o novo nó, aonde ocorrerá a remoção.
     Remova r de R
Se ch(R) <= d ou R é Raiz (Quase OK)
     Se R é Raiz e r era a última chave de R
           Retirar Raiz.
           Se Raiz não era folha
                 Filho da Raiz passa a ser a nova Raiz.
                 (Raiz só deve ter um filho, resultado de uma concatenação).
     Fim.
Senao
    Se R tem irmão adjacente S e ch(R)+ch(S) < 2d
          Efetuar Concatenação
          Propagar teste para o pai
    Senão
          Efetuar Redistribuição
          Fim.

Concatenação: Agrupar irmãos adjacentes num único nó, passando uma das chaves do nó pai (aquela está entre os dois ponteiros adjacentes que apontam para os irmãos) para este novo nó.

Redistribuição: Concatenação do irmão adjacente seguida de cisão.
 

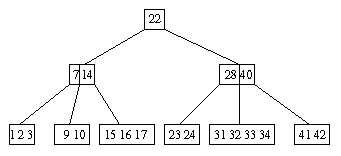
	Árvore Inicial Antes de Remover 70
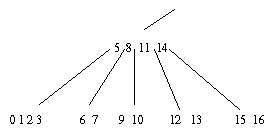
	70 Trocado pelo Sucessor (72) Retirado 70 da Folha
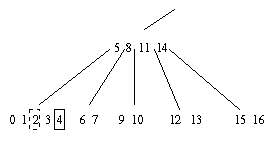
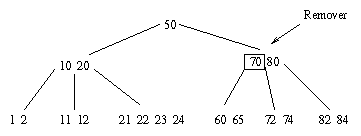
	Concatenação:  (74)+80+(82 84)
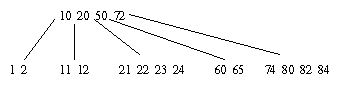	Concatenação: (10 20)+50+(72) Árvore perde um nível
	Nova Remoção: (Chave 60)
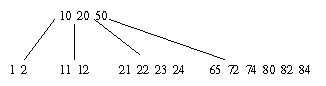	Redistribuição (1a Parte - Concatenação - (65) + 72 + (74 80 82 84))
	Redistribuição (2a Parte - Cisão - ''Sobe'' 74)

Material de Apoio