Revisão e Introdução

Tipos de dados

• Operação: Aritméticas, Inserção, Remoção, Ordenação, Máximo, Mínimo, Inversão, Transposição, etc.

Tipos abstratos de dados

Avaliação de desempenho de um algoritmo

• Dificuldade para reproduzir experimentos (ambientes multitarefa, compiladores, sistemas operacionais, etc).
• Necessidade de implementação do algoritmo.

• Aproximações através de modelos matemáticos.
• Não depende de implementações.
• Resultados podem não ser relevantes na prática.

Análise de complexidade de algoritmos (introdução bastante informal)

• Estimativa do tempo de execução (passos - operações atômicas)
• Tamanho de um problema
• Pior caso, melhor caso e caso médio
• Análise assintótica
• Ordem O, Omega e Theta (link interessante)
• Algumas classes importantes de funções:
• O(1) - Constante
• O(logn) - Logarítmico
• O(n) - Linear ou Polinomial de Ordem 1
• O(n²) - Polinomial de Ordem 2
• O(n³) - Polinomial de Ordem 3
• O(2ⁿ) - Exponencial
 

Algoritmo	Complexidade	2	10	100	10.000
A	f(n)=1000	1000	1000	1000	1000
B	f(n)=200logn	200	600	~ 1.200	~ 2.600
C	f(n)=50n	100	500	5.000	500.000
D	f(n)=n²	4	100	10.000	100.000.000
E	f(n)=2n	4	1024	1030	103010

Observações
• 1 dia ~ 10¹⁴ns
• 1 ano ~ 10¹⁶ns
• 2000 anos ~ 10¹⁹ns

  Gráfico ilustrando comportamento assintótico de certas classes de funções

  
• Para gerar o gráfico acima utilizando o SciLab faça download do arquivo assintotico.sci e execute-o utilizando o comando exec(assintotico.sci)

  Exemplo:

  Algoritmo: Busca Elemento
  Entrada: S[1],...,S[n] e elemento x a ser procurado.
  Saida: Booleano indicando se x está ou não no vetor.
  Funcao Busca(S[],x)
  para i:=1,...,n faca                  ; c1
  se S[i] = x entao          ; c2
  retorna Sim       ; c3
  retorna Não                           ; c4

Complexidade melhor caso = O(1)
Complexidade pior caso = O(n)
Complexidade caso médio = O(n) [demonstração utiliza estatística].

Cálculo pior caso:
f(n)     =  (n+1)*c1 + n*c2 + 0*c3 + 1*c4  ; c1=c2=...cm = 1
           =  (n+1)*1 + n*1 + 0 +1   = 2n + 2 = O(n)

Prova: c = 3 e n' = 2

Cálculo melhor caso:
f(n)=1+1+1+0=3=O(1)

Algumas das propriedades das funções O (Big O)
Se f = O(g) e g = O(h) entao f = O(h)

n = O(n²)
n² = O(n³)
logn = O(n)
1 = O(n)
n³ = O(2^n)

O(g+h) = O(g) + O(h)
O(kg) = kO(g) = O(g)

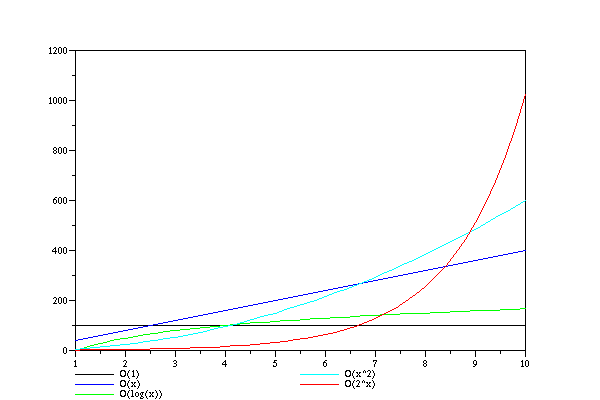
f = 3n + n^3 + logn = O(n) + O(n³) + O(logn) = O(n³)+O(n³)+O(n³) = 3O(n³) = O(n³).

Algoritmos ótimos

O Limite inferior g de um problema P é uma função tal que a complexidade (no pior caso), de qualquer algoritmo que resolva o problema P, está limitada inferiormente, assintoticamente, pela função g. (denota-se por Omega(g) a classe de funções limitadas inferiormente por g).
Qualquer algoritmo com complexidade O(g) é chamado de ótimo (sempre em relação a algum problema P). Note que o algoritmo ótimo está limitado superiormente (big O) e inferiormente (Omega) por g.
 

Resultados e constatações interessantes (que serão aprofundadas em disciplinas específicas na área da teoria da computação):

• Existem algoritmos ótimos para alguns problemas importantes.
• Existem problemas importantes inerentemente exponenciais.
• Existem problemas importantes para os quais não se conhece algoritmos que não sejam exponenciais, embora também não se tenha demonstrado a impossibilidade desses algoritmos existirem.

  Outro exemplo de cálculo de complexidade

  Algoritmo: Ordenação por inserção.
  Entrada: S[1]...S[n]
  Saida: Vetor S ordenado.
   

  funcao Ordenacao-por-Insercao(S)      para j:=2,...,n faca                            ; c1          chave := S[j]                                ; c2          i := j - 1                                       ; c3          enquanto i > 0 e S[i] > chave faca   ; c4              S[i+1] := S[i]                          ; c5              i := i - 1                                  ; c6          A[i+1] := chave                          ; c7

  void Ordena(int * S, int n)  {     int chave,i,j;       for(j=2;j<=n;++j)     {        chave = S[j];        i = j - 1;        while(i>0 && S[i]>chave)        {           S[i+1] = S[i];           --i;        }        S[i+1] = chave;     }  }

  Exemplo Execução:

  _5  2*  4  6   1   3
  2  _5   4* 6   1   3
  2   4   5  _6* 1   3
  _2 4   5   6    1* 3
  1   2  _4  5   6    3*
  1   2   3   4   5    6
   

  Complexidade do melhor caso: (while sempre falha)
   
  c1*n + c2*(n-1) + c3*(n-1) + c4*Sum(j:=2,...,n de t(j)) + c5*Sum(j:=2,....n de t(j)-1) +
  c6*Sum(...,t(j)-1) + c7*(n-1) =
  n+3*(n-1)+Sum(t(j))+2*Sum(t(j)-1) =
  Melhor caso: t(j) = 1 para j:=2,...n por isto
  Sum(t(j)) = Sum(j:=2,...,n de 1) = n - 1
  Sum(t(j)-1) = Sum(0) = 0
  n+3n-3+(n-1)+(n-2) = 6n-6 = O(n)

  Complexidade no pior caso: (while falha em i >0)

  Apenas t(j) muda.
  t(j) = j , para j := 2,...,n

  Sum(j:=2,...,n de j) = Sum(j:=1,...,n de j) - 1 = n/2*(n+1)-1
  Sum(j:=2,...,n de j-1) = Sum(j:=1,...,n-1 de j) = n*(n-1)/2