Busca binária X busca seqüencial

Busca Seqüencial (74) - Comparações com 2 , 4 , 7 , 9 , 20 , 30 , 35 , 50 , 58 , 66 , 68 , 70 , 72 , 73 , 74
Busca Binária (74) - Comparações com 58 (S[9]) ,  72 (S[13])  ,   74 (S[15).

Árvores Binárias

Uma árvore binária T é um conjunto finito de nós, tal que:
• T = nil ( a árvore é dita vazia ), ou
• Existe um nó r, chamado raiz de T, e duas subárvores T^E(r) e T^D(r), chamadas subárvores Esquerda e Direita de r, que também são árvores binárias.

 

Árvore  Vazia  ( )	(A () ())	(A (B () () ) ())	(A (B () ()) (C () ())	(A (B () ()) (C (D () ()) ()))
Árvore T1	Árvore T2	Árvore T3	Árvore T4	Árvore T5

Definições Auxiliares

Quando a subárvore T' de um nó r não é vazia, dizemos que a raiz r' de T' é filho do nó r.
Além disto, r é chamado de pai de r'.
Usamos também os termos, filho esquerdo e filho direito, para distinguir os dois filhos de um nó.
Filhos de um mesmo pai são chamados de irmãos.
De maneira analoga, podemos definir os conceitos de tio, primo, avo, descendente e ancestral.
Nós sem filhos são chamados de folha.
Caminho:  Sequência de nós distintos v₁, v₂, ..., v_k tais que, para todo 0 < i < k  temos que v_i é filho de v_i+1 ou então, para todo 0 < i < k  temos que v_i é pai de v_i+1
O comprimento de um caminho é k-1.
Nível de um nó é "o comprimento do caminho da raiz té o nó" + 1.
Altura de um nó é "o comprimento do maior caminho do nó até um dos seus descendentes" + 1.
Altura de uma árvore é a altura da raiz da árvore.
Árvore: Quando o número de subárvore de r pode ser maior que 2.
Árvore Ternária: Quando r possui exatamente 3 subárvores.
Árvore Quaternária: Quando r possui exatamente 4 subárvores.
Árvore estritamente binária: Cada nó possui exatamente 0 ou 2 filhos.
Árvore binária completa: Nós com menos de 2 filhos ficam no úlimo ou no penúltimo nível da árvore.
Árvore binária cheia: Nós com menos de 2 filhos ficam no último nível da árvore.

Usando as definições: (Exemplos se referem as árvores da ilustração acima).

As árvores T1 e T4 são cheias, completas e estritamente binárias.
As árvores T3 e T5 são completas mas não são cheias.
O nó D da árvore T5 é folha, é filho do nó C, tem nível 3 e altura 1.
Todas as folhas de uma árvore tem altura 1.
O nó A da árvore T5 é avo do nó D.

Representação usando ponteiros:


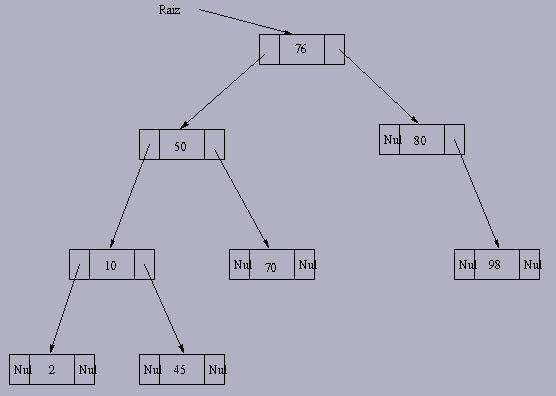
* Representação por parênteses aninhados: (76 (50 (10 (2 () ()) (45 () ())) (70 () ())) (80 () (98 ()())))

Struct SNo  /* Estrutura que pode ser usada na construção de uma árvore em C */
{
    int Chave;
    SNo * FilhoEsq;
    SNo * FilhoDir;
};

SNo * Raiz;

Percurso em profundidade

Pré-ordem*	Ordem Simétrica*	Pós-ordem*
void Percorre(SNo * r)  {     visita(r);     if( r->FilhoEsq != NULL)     {         Percorre(r->FilhoEsq);     }     if( r->FilhoDir != NULL)     {         Percorre(r->FilhoDir);     }  }	void Percorre(SNo * r)  {     if( r->FilhoEsq != NULL)     {         Percorre(r->FilhoEsq);     }     visita(r);     if( r->FilhoDir != NULL)     {         Percorre(r->FilhoDir);     }  }	void Percorre(SNo * r)  {     if( r->FilhoEsq != NULL)     {         Percorre(r->FilhoEsq);     }     if( r->FilhoDir != NULL)     {         Percorre(r->FilhoDir);     }     visita(r);  }
76 - 50 - 10 - 2 - 45 - 70 - 80 - 98	2 - 10 - 45 - 50 - 70 - 76 - 80 - 98	2 - 45 - 10 - 70 - 50 - 98 - 80 - 76

* Note que estes códigos não funcionam quando a árvore é vazia. Uma alternativa poderia ser: (Para pós-ordem, por exemplo)

void Percorre(SNo * r)
{
   if( r != NULL )
   {
        Percorre(r->FilhoEsq);
        Percorre(r->FilhoDir);
        visita(r);
   }
}

Exercício: implementar algoritmos de percurso em profundidade utilizando uma pilha explícita ao invés de recursão.

Percurso em largura

• Nós são percorridos nível a nível (primeiro todos os nós do nivel 0, depois todos os do nível 1, depois todos os do nível 2, e assim sucessivamente).
• Algoritmo similar ao percurso em pré-ordem (com pilha explícita), mas trocando a pilha por uma fila:
  
  void Percorre()
  {
     while(!fila.vazia()) {
       SNo * r = fila.retira();
       visita(r);
       if(r->FilhoEsq) fila.insere(r->FilhoEsq);
       if(r->FilhoDir) fila.insere(r->FilhoDir);
     }
  }

  Altura da árvore.

  Com uma pequena alteração no percurso em pós-ordem podemos obter um algorítmo que devolve a altura de uma árvore binária:

  int Altura(SNo * r)
  {
     int AlturaE , AlturaD;

     if( r != NULL )
     {
         AlturaE = Altura(r->FilhoEsq);
         AlturaD = Altura(r->FilhoDir);
         if( AlturaE > AlturaD ) return( AlturaE + 1);
         else return(AlturaD + 1);
     }
     else return(0);
  }

  Lema 1: Em uma árvore binária T com n > 0 nós, o número de sub-árvores vazias, v(T), é n + 1.
  Prova: (Por indução em n).
  Base: (n=1)

  Neste caso, temos apenas os dois filhos vazios da raiz.
  Portanto, v(T) = 2 = n + 1.
  Passo: (n>1)
  Vamos supor que o lema seja verdadeiro para árvores com k < n nós. (Hipótese de Indução)
  Como o número de nós de uma árvore é finito, temos que, existe pelo menos um nó x sem nenhum filho.
  Seja T' a árvore obtida removendo-se o nó x de T.
  T' é uma árvore binária, visto que x foi apenas substituido por uma árvore vazia.
  Além disto, T' possui  n' = n -1 nós.
  Portanto, pela hipótese de indução, v(T') = n'+1.
  Agora, v(T) é v(T') mais as duas sub-árvores vazias de x, menos a sub-árvore vazia que foi acrescentada em T' no lugar de x.
  Portanto, v(T) = v(T') + 2 - 1 = v(T') + 1 = n' + 1 + 1 = n - 1 + 1 + 1 = n + 1.
  Lema 2: Uma árvore binária completa T, com n > 0 nós, possui altura h(T) mínima.
  Prova: (Por absurdo)
  Vamos supor por absurdo que exista uma árvore binária completa, com n nós, que não tenha altura mínima.
  Seja T a menor, em altura, destas árvores.
  Temos então que existe uma árvore binária não completa, T', com n nós e altura mínima h(T') menor que h(T).
  Agora, retirando-se nós do último nível de T' e substituindo as sub-árvores vazias do nós que se encontram acima do penúltimo nível por estes nós, obteremos uma nova árvore completa T'', com n nós.
  Como não foi acrescentado nenhum nó acima do último nível de T', temos que h(T'') <= h(T').
  Como h(T') é mínimo, temos que h(T'') >= h(T'').
  Logo,  h(T'') = h(T').
  E portanto, a altura da árvore completa T'' é menor que h(T).
  Absurdo, visto que escolhemos T como sendo a de menor altura entre todas as completas.
  Lema 3: A altura h de uma árvore binária completa T é 1 + |_  log n  _|
  Prova: (Por indução em n)
  Base: (n=1)
  h = 1 = 1 + 0 = 1 + |_ log 1 _| = 1 + |_ log n _|
  Passo: (n>1)
  Vamos supor que o lema seja verdadeiro para árvore com k < n nós (Hipótese de indução)
  Seja T' a árvore obtida ao retirarmos todos os nós do último nível de T.
  Seja p o número de nós retirados de T.
  Por construção, a árvore T' é cheia.
  Além disto, T' possui n' = n - p nós.
  Pela hipótese de indução, h(T') = 1 + |_ log n' _|
  Como T' é cheia, n' = 2^m - 1, para algum inteiro m > 0.
  Ou seja, h(T') = m
  Temos ainda que k >= 1, visto que o último nível de qualquer árvore não vazia deve conter pelo menos 1 nó.
  E além disto k <= n'+1, uma vez que apenas os nós do último nível de T' podem ter sub-árvores vazias e pelo Lema 1, o total de sub-árvores vazias de T' deve ser n'+1.
  Deste modo,
  h(T) = 1 + h(T') = 1 + m = 1 + log(n'+1) = 1 + |_ log(n'+k) _| = 1 + |_log n _|
  * Perceba que a introdução do piso só possível porque sabemos que 1 <= k <= n'+1. e que n' =  2^m - 1, para algum inteiro m > 0.