
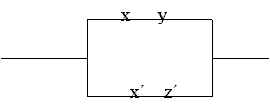
Correção: trocar x' z' por x' z
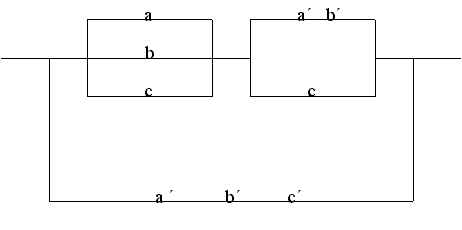
Correção: O circuito acima está representando a seguinte
expressão: (a+b+c).(a'b'+c)+a'b'c' [e não aquela do exercício]
* Lembre-se das prioridades entre os operadores na hora de decidir se deve-se ou não usar parênteses. Nas respostas acima usamos parênteses apenas quando estritamente necessário.
a)
 |
b)
 |
c)
 |
d)

Correção: trocar x' z' por x' z |
e)
 |
f)
 |
|
|
g)
 |
|
|
h)

Correção: O circuito acima está representando a seguinte expressão: (a+b+c).(a'b'+c)+a'b'c' [e não aquela do exercício] |
Aguardo respostas corretas (arquivos .gif ou jpg) para os exercícios d, h e i.
a)
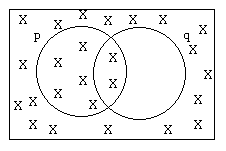
|
b)
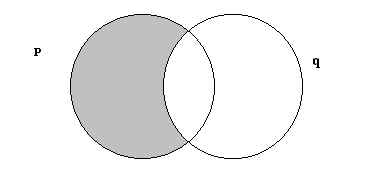 |
c)
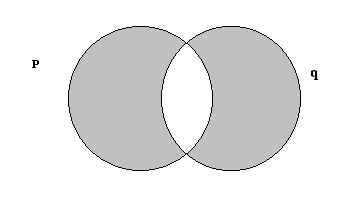 |
d)
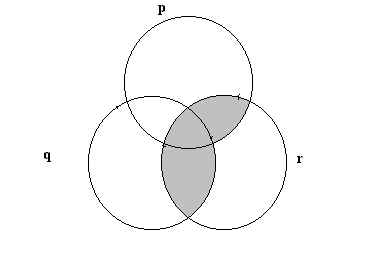 |
e)
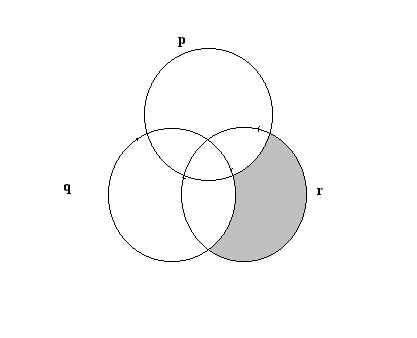 |
f) Igual a letra d. !!!
|
Dica: Para testar suas respostas tente encontrar algebricamente expressões equivalentes e verificar se os diagramas são iguais (devem ser).
* Caso suas respostas não estejam exatamente iguais as fornecidas acima, use as relações de equivalência (manipulação algébrica) para provar (verificar) que as suas respostas são equivalentes a estas.
a)