Teoria dos Grafos - Grafos Planares

---

Grafos Planares

Admitem representação no plano sem que as arestas se cruzem

Exemplo K4 Mostre que K_2,3 é planar {Basta mostrar uma representacao planar, ou seja, basta desenhar o grafo de maneira em que as arestas nao se cruzem}
   

Problema da Água, Luz e Telefone: Distribuir água,luz e telefone a cada uma das três casas sem que as ligações entre
elas se cruzem

Modelando o problema, água,luz, telefone e casa tornam-se vértices, e as ligações arestas,
o problema passa a ser encontrar umarepresentação planar para o grafo abaixo:
   

O grafo acima mostrado é o grafo K_3,3   .

Teorema k_3,3 não é Planar ( I )

• Curva de Jordan, é uma curva fechada.

Exemplos:
 

É  CJ	É CJ	Não é CJ	Não é CJ

 

Teorema da "Curva de Jordan"

Seja J uma Cuva de Jordan
Seja int J a região interior a J
[
Seja ext J a região exterior a J

Teorema: Qualquer "linha" com uma extremidade em int J e outra em ext J, intercepta J em algum ponto

  { Se voce tem um ponto dentro da curva e outro fora, voce pode passar um linha ligando estes pontos e esta linha passa pela curva}

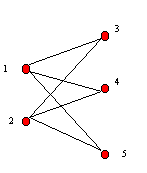
Vamos supor por absurdo que K_3,3 é planar
Seja G uma representação planar de  K_3,3
Seja X, Y a bipartição de G.{Provar que um grafo bipartido completo só tem uma bipartição}
Sejam v₁,v₂,v₃ os vértices em X, e u₁,u₂,u₃ os vértices em Y, temos então que:

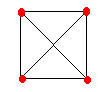
AG={ (v₁,u₁),(v₁,u₂),(v₁,u₃),(v₂,u₁),(v₂,u₂),(v₂,u₃),(v₃,u₁),(v₃,u₂),(v₃,u₃)}

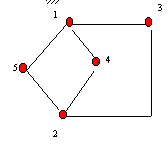
O ciclo C={v₁,u₁v₂,u₂,v₁}é uma curva de Jordan em G
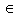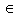Agora, ou u₃int C, ou u₃ext C
Supondo, sem perda de generalidade, que u₃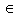int C{Se ele estivesse fora eu poderia renomear de outra maneira}

 
   

Temos então que o "caminho" {v₁,u₃,v₂} divide int C em duas regiões

C₁: {u₁,v₁,u₃,v₂,u₁}
C₂: {u₂,v₁,v₃,v₂,u₂}

Existem apenas 3 possibilidades para o posicionamento de v₃:

Caso1:

v₃ 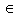ext C e portanto, pelo teorema da Curva de Jordan
(v₃,u₃) intercepta C.
Absurdo, visto que G é uma representação planar.{Não permite que arestas se cruzem}

Caso2:

v₃ 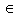int C₁ e portanto, (v₃,u₂) intercepta  C₁
Absurdo.

Caso3:

v₃ 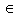int C₂ e portanto, (v₃,u₁) intercepta  C₂
Absurdo.

Provar que k₅ não é planar