Isomorfismo

Definição

Dois grafos G e H são ditos isomorfos se existirem duas funções bijetivas f: VG->VH e g: AG->AH tais que para cada aresta de G, com extremos u e v, os extremos de g() são f(u) e f(v).
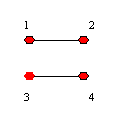
O par (f,g) de funções é um isomorfismo de G em H.
Pode existir mais de um isomorfismo entre dois grafos.
Denota-se que G é isomorfo a H por G  H
 

Isomorfismo em Grafo Simples

Em grafos simples, a definição de f:VG->VH, com a propriedade de manutenção das adjacências, determina totalmente o isomorfismo.

Provando que dois grafos G e H são isomorfos:

 Exemplo:

 

Grafo G	Grafo H

VG = {1,2,3,4} e AG = {(1,2),(3,4)}
VH = {a,b,c,d} e AH = {(a,d),(b,c)}

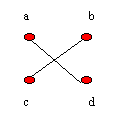
Sejam a funcao f:VG->VH assim definida: {(1,a),(2,d),(3,b),(4,c)}
e a função g:AG->AH definida por { ((1,2),(a,d)) , ((3,4),(b,c)) }

Pela definição de f e g, estas funções são bijetivas. Além disso,
g((1,2)) = (a,d) = (f(1),f(2)) e
g((3,4)) = (b,c) = (f(3),f(4))

Logo, o par de funções f e g é um isomorfismo de G em H e portanto G e H são isomorfos.

Provando que dois grafos G e H não são isomorfos

Exemplo:
  VG = {1,2,3,4} e AG = {(1,2),(2,4)}
VH = {a,b,c,d} e AH = {(a,d),(b,c)}

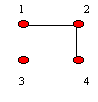
Vamos supor por absurdo que G e H sejam isormorfos.

Seja f, g um isomorfismo de G em H.
Temos então que :

g((1,2)) = (f(1), f(2)) e
g((2,4)) = (f(2), f(4)).


Como f e g são bijetivas, temos duas arestas distintas em H,
((f(1),f(2)) e (f(2),f(4)), com um vértice em comum, f(2).

Absurdo, pois todos os vértices de H tem grau 1.