 |
 |
|
|
|
|
|
|
|
|
|
 |
 |
|
|
|
|
|
|
|
|
|
Família: Diferente de conjunto, uma família permite elementos duplicados.
Par não ordenado: (a,b) = (b,a)
Grafo Trivial é aquele em que VG é um conjunto unitário e AG =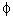
Grafo Identidade de G é um grafo H tal que VG=VH e AG=AH
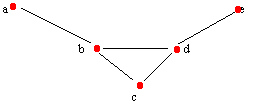
Seja G um grafo e= (a,b)
AG.
Definimos:a e b são os extremos da arestaArestas Adjacentes são duas arestas com um extremo em comum .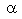
a e b são vértices adjacentes
é incidente a a e b
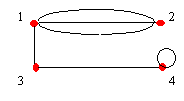
Arestas Múltiplas são arestas que possuem os mesmos extremos. ( os dois )
Laço é uma aresta cujos extremos são iguais ( Ex.: (4,4) )
Tamanho de um grafo G = |VG|+|AG| (uma das possíveis definições)
Obs: Usaremos, neste texto, n para indicar |VG|, e m para indicar |AG|
Quando a família de arestas é formada por pares ordenados dizemos que o grafo é orientado ou direcionado.
Nesse caso, ao desenhar o grafo, devemos usar uma seta partindo do primeiro elemento do par até o segundo:
Os grafos G1 e G2 são diferentes , /* Se não fossem orientados seriam iguais */
VG1 = { a,b,c }. VG2 = { a,b,c }. AG1 = { (a,b) , (b,c) } AG2 = { (a,b) , (c,b) }
Um grafo simples é um grafo que não contém nem laços nem arestas múltiplas.Ex: Grafo Touro.
Os grafos abaixo Não são exemplos de grafos simples:
Laço (a') Arestas Múltiplas (b' b'')
O grafo é representado por uma lista de listas .Exemplo:
Obs. Se o grafo fosse orientado a primeira coluna da tabela acima seria a origem, e a segunda o destino das arestas.
Vértices Vértices aos quais estão ligados 1 2 4 5 2 1 3 3 1 2 4 5 3 4
Grafo G,
1 2
4
5
21
3
31
2
4
53
4
VG ={1,2,3,4,5}
AG ={ (1,2), (1,4), (1,5),(2,1),(2,3),(3,1),(3,2),(5,3),(5,4)}
O grafo orientado é representado por uma matriz quadrada, nXn, em que n é o número de vértices do Grafo.
Indicamos a existência de uma aresta saindo de vértice i e chegando em um vértice j , colocando o número 1 na linha i, coluna j, da matriz. (Na matriz abaixo, por exemplo, existe a aresta (1,2), mas não existe a aresta (2,1))Exemplo:
Grafo G,VG ={1,2,3,4}Se o grafo é simples e não orientado, não aparecem "uns" na diagonal principal e
AG ={ (1,2), (1,4), (2,2), (2,3), (2,4), (3,1), (4,2), (4,3)}
a matriz é simétrica em relação à diagonal principal.
Exemplo:
Grafo G,VG ={1,2,3,4}
AG ={ (3,1), (3,2), (4,2), (4,3)}
Grafo G,
VG ={1,2,3,4}
AG ={ (1,2), (1,3), (1,3),(2,4),(4,3)}
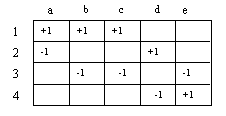
O Complemento de um grafo simples G, denotado por G', é o grafo simples que possui o mesmo conjunto de vértices de G, e tal que dois vértices distintos são adjacentes em G' sse não são em G.
Touro Touro Complementar
VG = {a,b,c,d,e}
VG = {a,b,c,d,e} AG={(a,b),(b,c),(b,d),(d,e),(c,d)} AG={(a,e),(a,c),(c,e),(a,d),(b,e)}
|
|
|
|
|
|
|
|
|
 |
 |
 |
 |
|
|
|
|
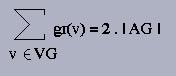 |
Prova:
Seja A= ![]() v
v ![]() P gr(v)
e B=
P gr(v)
e B=![]() v
v ![]() I gr(v)
I gr(v)
Obs: Note que a prova acima utiliza diversos teoremas da arimética (Eg.: A soma de dois numeros pares é um número par, a soma de um número ímpar e um número par é ímpar, ...)
Seja A= ![]() gr(v) , somatório
de i =1 até n
gr(v) , somatório
de i =1 até n
Como a soma de uma quantidade ímpar de números
ímpares
é ímpar, temos que A é ímpar
Seja B a soma dos graus dos vértices de grau par.
Como a soma de números pares é par, temos então
que B é par
Como a soma de um par com um número ímpar é
ímpar,
temos que A + B é ímpar.
Ou seja, a soma dos graus dos vértices de G é ímpar.
Absurdo, visto que pelo teorema da soma dos graus, a soma dos graus de um grafo é par.
Teoremas:
Todo Grafo Ciclo Cn é 2-regular,
Todo Grafo com AG =![]() é 0-regular,
é 0-regular,
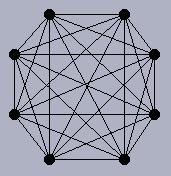
Todo Grafo Completo Kn é (n-1) k-regular.
|
|
|
|
|
Prova:
Seja G um grafo k-regular.Prova:
No Kn todos os vértices tem grau (n-1), uma vez
que
cada vértice está ligado a todos os n vértice de
G,
com exceção dele mesmo.
Pelo teorema anterior temos que n.k = 2m.
Substituindo k por (n-1) temos que n.(n-1) = 2m
Logo, m = n(n-1)/2
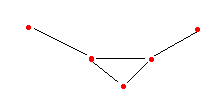
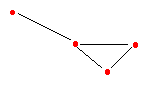
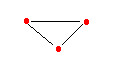
Denotamos esse grafos por G[VH].
Exemplo:
Dado G = ({a, b, c, d, e}, {(a, b), (b, c), (b, d), (d, e), (c,
d)}).
H1 = ({a, b, c}, {(a,b), (b, c)}) = G [a, b, c] é
um subgrafo induzido de G.
 |
 |
 |
|
|
|
|
Prova:
Vamos supor por absurdo que exista tal grafo G.
Seja v10 o vértice de G que possui grau 9.
(A sequência s mostra que este vértice existe).
Como o número de vértices de G é 10, v10
deve ser adjacente a todos os outros vértices de G.
Seja G' = G\v10 /* G menos o vértices v10 */ um subgrafo induzido de G.
A sequência de Graus de G' só pode ser
0,0,2,2,2,2,4,5,7.
(Como v10 estava ligado a todos os vértices, com
a sua retirada, todo os vértices perdem 1 unidade em seus
graus).
G' possui um vértice v com grau 7.
Portanto, 8 vértices de G' devem ter grau ![]() 1. (Lembre-se que v é simples).
1. (Lembre-se que v é simples).
Absurdo, visto que a sequência de G' só possui 7
vértices
com grau ![]() 1.
1.
Exemplos: Ser um grafo Simples, Ser cordal, Completude (Ser
Completo).
Não exemplos: k-regularide (ser k-regular).