 |
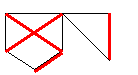 |
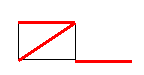
| Cobertura com 3 arestas | Cobertura com 4 arestas |
 |
 |
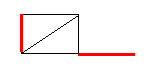
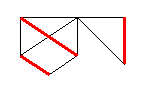
| Cobertura com 3 arestas | Cobertura com 4 arestas |
 |
 |
{Cada aresta cobre dois vértices distintos}
Obs: viz(X) = conjunto de vértices
adjacentes a X (vizinhança de X)
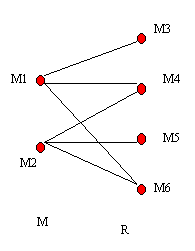 |
X = {M1} viz(M1) = M3, M4, M6
Para provar que não existe
emparelhamento
que cobre M, encontrar um conjunto > que a vizinhança
Base: ( |VG| = 2 )
Hipótese de Indução:
Passo: ( |VG| > 2 )
Caso 1:
Caso 2:
Temos então que:
Para todo X ⊂ S , |vizH(X)|
≥
|X| , uma vez que vizH(X) = vizG(X)
Portanto, pela H.I, existe um
emparelhamento tH
que cobre S em H.
Temos ainda que:
E portanto, pela HI, existe um emparelhamento tK que cobre M\S em
K
tH ∪ tK ∪ α
é um emparelhamento em G
É possível casar todas as moças de uma vila com um rapaz de quem ela gosta ?Transcrição para Teoria dos Grafos:
Tomamos um grafo bipartido G de tal forma que exista uma bipartição { M,R } onde cada vértice de M representa uma moça e cada vértice de R representa um rapaz, usamos as arestas para representar a relação de "gostar" . O problema passa a ser determinar se G tem um emparelhamento que cobre M.
O Teorema da Hall nos diz que a solução é positiva se e somente se para qualquer X ⊂ M , |viz(X)| ≥ |X|.
Um emparelhamento máximo é um emparelhamento t* em G tal que G não contém outro emparelhamento com |t| > |t*|Vértice Livre
Um vértice v é livre, com relação a um emparelhamento t, se v não é extremo de nenhuma aresta de t.Caminho AlternanteUm caminho alternante em relação a um emparelhamento t é um caminho cujas arestas estão alternadamente em AG\t e t ( onde t é um emparelhamento). // AG\t = Conjunto de arestas que nao estao no emparelhamento.Caminho de Aumento
Exemplos:
Vertice Livre: 1
Caminho Alternante:( 1,2,3,4,5), (3,4,5),(1,2),(4,5)É um caminho alternante com ambos os extremos livres.
Exemplos:
Vertice Livre: 1,6,7
Caminho de Aumento (Caum): (6,5,4,7),(1,2,3,4,5,6)
t é máximo sse Não existir um caminho de aumento em relação a tAlgorítmo para Encontrar Emparelhamento Máximo
Existe um caminho de
aumento, então este
emparelhamento não é
máximo. Caum=(6,3,4,5)Não exite caminho de
aumento, então o
emparelhamento é máximo
tum emparelhamento qualquer (Vazio) {Começa com vazio}
CCaminho de aumento em relação a t // Algoritmo para encontrar este caminho e' apresentado logo abaixo.
Enquanto existir caminho de aumento faça
t{ t -C}
{ C - t} {Faco um novo emparelhamento com as arestas que estavam em t menos as arestas do caminho e as arestas do caminho menos as arestas que estavam em t}
CCaminho de aumento em relação a t{Achar novo caminho de aumento em relação a t}
Sejam {M,R} a bipartição de GPasso 1: Construa todos os caminhos de tamanho 1, com arestas (Mi,Ri) que não estejam no emparelhamento, e que tenha um vertice livre em M.
Passo 2: Partindo dos caminhos gerados no passo anterior , procure aqueles que podem ser estendidos com arestas (Ri,Mi) que estejam no emparelhamento t, e que ainda não tenham sido usadas no caminho.
Passo 3: Partindo dos caminhos gerados no passo anterior ,procure estende-los com arestas (Mi,Ri) que ainda não estejam em t e não estejam no caminho.
Continue aumentando o tamanho dos caminhos, seguindo os passos 2 e 3, até chegar a uma destas duas situacoes:
Caso 1: Foi acrescentada uma aresta (Mi, Rj) com Ri livre e consequentemente, ja temos um caminho de aumento.
Caso 2: Nao e' possivel mais aumentar o tamanho dos caminhos e portanto, nao existe caminho de aumento em relacao ao emparelhamento atual.
Exemplo:
1 2 3 4 5 ... (M2,R1) - (M2,R2) - (M2,R4) (R4,M3) (M3,R2)