Teoria dos Grafos - Conectividade
Definições Auxiliares
Passeio
Um passeio P de v0 a vn
, é uma sequência finita e não vazia ( v0 , 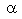 1,
v1 ,
1,
v1 , 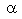 2
,
v2, ......,
2
,
v2, ......,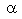 n,
vn ), cujos elementos são alternadamente
vértices
e arestas de um grafo G, e tal que
n,
vn ), cujos elementos são alternadamente
vértices
e arestas de um grafo G, e tal que 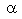 i
= (vi-1,
vi). para 1
i
= (vi-1,
vi). para 1 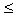 i
i 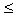 n
.
n
.
Passeio degenerado: Quando n = 0. /*Passeio com um
único
vértice*/
Passeio fechado: Quando n > 0 e v0 = vn .
/* Começa e termina no mesmo vértice */
Comprimento do passeio = n /* Total de arestas no
passeio
*/
Dado o grafo
Touro,
um exemplo de passeio é
a,(ab),b,(bc),c,(cd),d,(db),b,(bc),c,(cb),b.
Um passeio fechado poderia ser: a(ab)b(bd)d(db)b(ba)a /*
Começa
e termina em a */
Dados dois passeios P = (v0,(v0,v1),v1,(v1,v2),...,(vn-1,vn),vn)
e Q = (w0,(w0,w1),w1,(w1,w2),...,(wm-1,wm),wm)
tais que vn = w0, definimos PQ como sendo a
justaposição
do caminho P e Q. /* Acrescentamos o passeio Q "na frente" de P */
Trilha
Passeio em que as arestas são duas a duas distintas.
(vertices
podem ser repetidos)
Ex: (ainda no grafo Touro): a,(a,b),b,(b,c),c,(c,d),d,(d,b),b
Trilha Fechada:
começa e termina no mesmo vértice.
Caminho
Trilha em que os vértices são dois a dois
distintos.
(e consequentemente as arestas)
(Não repete arestas nem vértices)
Dados dois vértices u e v de um grafo qualquer G,
denomina-se caminho mínimo de u a v, o menor caminho,
em G, ligando u a v.
Grafo Caminho - Pn
Grafo simples em que existe um caminho que passa por todos os
vértices
de G
Ciclo ou Circuito
Trilha fechada em que v1,...,vn-1
são
dois a dois distintos. Note que, informalmente, poderiamos dizer que um
ciclo é simplesmente um caminho fechado, mas então
teríamos um problema
com a definição de caminho, pois, um caminho não
pode
ter vértices repetidos.
Grafo Circuito ou Ciclo - Cn
Grafo simples em que existe um ciclo que passa por todos os
vértices
de G
Passeios em grafos simples
Em um grafo simples qualquer tipo de
passeio
pode ser representado apenas pelos vértices, uma vez que existe
no máximo uma aresta ligando dois vértices.
Alguns Teoremas
Qualquer caminho "contido" em um caminho mínimo é
também mínimo
Teorema:
Seja P = ( u0,u1,...,un
)
um caminho mínimo de uo a un.
Então, o caminho Q = (ui,ui+1,....,ui+m
),
i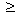 0
e i
+ m
0
e i
+ m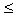 n, é
um caminho mínimo de ui a ui+m
n, é
um caminho mínimo de ui a ui+m
Prova:
Seja:
P = ( u0,u1,...,un )
um caminho
mínimo de uo a un e
S = (ui,ui+1,....,ui+k ), 0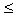 i
i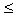 n
e i + k
n
e i + k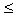 n.
n.
Vamos supor, por absurdo, que S não seja um caminho
mínimo
de ui a ui+k .
Logo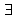 S'=(v0,v1,....,vm
)
,v0=ui e vm =ui+k
tal que, | S'| <| S |
S'=(v0,v1,....,vm
)
,v0=ui e vm =ui+k
tal que, | S'| <| S |
Sejam R= ( u0,...,ui ) e T=(ui+k,....,un
). Temos então que
| P | = | R | + | S | + | T |
O passeio P'=( u0,...,ui , v1,....,vm
,
ui+k+1 , ....., un
)
,
ligando u0 a un , existe, e tem comprimento
igual a | R | + | S'| + | T |.
Como | S' | < | S | temos que | P' | < | P |.
Como | P' | é um passeio e como todo passeio possui um caminho C' que tem
comprimento menor
que o comprimento do passeio (demonstrar), temos que | C'| <|
P'| , como
| P' | < | P | e | C'| <| P'| , entao | C'| < | P |.
Absurdo, visto que P é um caminho mínimo.
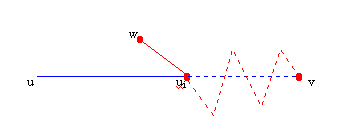
Todo passeio contém um caminho
Teorema: Se 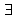 um passeio P de u
um passeio P de u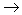 v
, então
v
, então 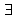 um
caminho C de u
um
caminho C de u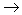 v.
v.
Demonstração: (exercício)
Ligaçao
Sejam G um grafo e u, v dois
vértices
de G.
Dizemos que u e v são ligados, ou conectados, sse 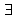 um
caminho C de u a v em G.
um
caminho C de u a v em G.
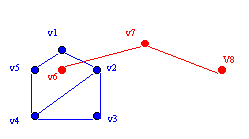 |
Ligados: v1e v3, v3 e v4,
v6 e v8, v7 e v8
Não Ligados:v1e v6,
v7 e v4
|
Lema: Ligação é uma relação de
equivalência
sobre VG
Revisão: Um relação é de equivalência
sse ela é reflexiva, simétrica e transitiva.
Demonstração:
Seja G um grafo qualquer com o conjunto VG de vértices e a
relação
L, de ligação, sobre este conjunto.
L é Reflexiva, pois para todo v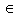 VG,
VG, 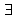 o
passeio degenerado <v> que é um caminho de v em v, e
portanto:
v é ligado a v.
o
passeio degenerado <v> que é um caminho de v em v, e
portanto:
v é ligado a v.
L é Simétrica, pois para todo v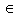 VG,
se
VG,
se 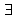 um caminho
C = < v0 , v1 , ......., vn >,
com u=v0 e vn =v, ligando u a v
então
um caminho
C = < v0 , v1 , ......., vn >,
com u=v0 e vn =v, ligando u a v
então 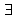 um
Caminho C' = < vn , vn -1 , ..., v0
> ligando v a u.
um
Caminho C' = < vn , vn -1 , ..., v0
> ligando v a u.
L é Transitiva, pois para todo u, v, w 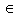 VG
temos , se
VG
temos , se 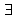 um
caminho P de u
um
caminho P de u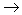 v
e um caminho Q de v
v
e um caminho Q de v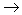 w
então existe um um passeio de u
w
então existe um um passeio de u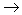 w. Demonstraremos essa
afirmação da seguinte forma:
w. Demonstraremos essa
afirmação da seguinte forma:
Sejam os caminhos
P = (u0, 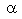 1,
u1, .....,
1,
u1, ....., 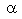 p,
up) , com u0 = u e up =
v.
e
p,
up) , com u0 = u e up =
v.
e
Q = ( v0, 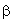 1,
v1,...,
1,
v1,..., 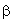 q,vq
)
, com v0 = v e vq = w.
q,vq
)
, com v0 = v e vq = w.
Seja i o menor inteiro tal que ui = vj ,
0 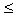 j
j 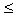 q
e 0
q
e 0 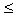 i
i 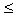 p.
p.
Temos então que P1 = (u0,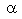 1,
u1,
1,
u1,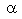 2,....,
2,....,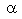 i, ui ) é um caminho de u0 a ui
e
i, ui ) é um caminho de u0 a ui
e
Q1 = (vj,vj+1,...,vq)
é
um caminho de vj a vq
Portanto, C = P1Q1 é um caminho de u
a
w. (Lembre-se que u0 = u e ui = vj e
vq = w.)
Teorema: Ligação induz Partição
Grafos Conexos
Dada a partição { V1,V2,...,Vk
}, induzida pela relação de ligação sobre
os vértices de um grafo G. Dizemos que os subgrafos induzidos G[V1],
G[V2] , ... , [Vk] são componentes
conexos de G.
Indicamos por C(G) o número de componentes conexos de G.
Dizemos que um grafo é conexo quando C(G)
= 1, caso contrário, o grafo é dito desconexo.
Obs. Não são somentes os grafos completos que
possuem
1 componente
conexo, exemplo
Partição:{1,2,3,4}
C(G)=1
Teorema: Se G é conexo então quaisquer 2
caminhos de
comprimento máximo em G tem um vértice em comum.
Demonstração:
(Exercício)
Problema: Demonstrar que, em qualquer grupo de 2 ou mais pessoas,
sempre
existem 2 com o mesmo número de amigos.
Modelando o problema para teoria dos grafos, temos:
VG: Grupo de pessoas, | VG| 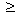 2
2
AG: Relação de amizade
Teorema: para qualquer grafo simples 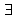 pelo
menos 2 vértices x,y tais que gr(x)=gr(y)
pelo
menos 2 vértices x,y tais que gr(x)=gr(y)
Prova:
Caso 1 :
Não existe componente conexa C com | V(C) | > 1
Temos então que C é um grafo vazio com pelo menos 2
vértices.
Logo, 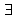 2
vértices x,y tais que gr(x) = gr(y) {Grau(x)=0=Grau(y)}
2
vértices x,y tais que gr(x) = gr(y) {Grau(x)=0=Grau(y)}
Caso 2 :
Demonstrar os seguintes teoremas
(exercícios):
(1) Qualquer grafo conexo com | V(G) | >1
não possui vértices de grau zero
(2) Todos os vértices de um grafo
conexo
G, com | V(G) | > 1, têm grau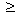 1
1
(3) Se G é conexo então
quaisquer
2 caminhos de comprimento máximo em G têm um
vértice em comum