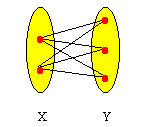
(I) Cada aresta G possui um extremo em X e outro em Y
Exemplo
 |
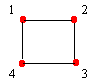Y={4,2}{Cada extremo de uma aresta tem que estar em um conjunto diferente}
Obs: Para demonstrar que um grafo G é bipartido basta mostrar uma bipartição de VG que satisfaz (I). No entanto, para mostrar que um grafo não é bipartido, não basta mostrar uma bipartição que não satisfaz (I), deve-se demonstrar que é impossivel encontrar uma partição que satisfaz a condição (I).
Exercício: Demonstrar que Kn , com n >= 3, não é bipartido. (Idéia: Todo Kn, com n>= 3, contém o subgrafo induzido K3 )
Resolução: Para um grafo ser bipartido
ele não pode ter ciclo ímpar, todos os grafos Kn com n
3,
possuem o subgrafo induzido K3 e este subgrafo possui um ciclo ímpar,
então os grafos Kn com n3
não são bipartidos pois todos possuem um ciclo ímpar.
):
Por Absurdo
X,
temos que
i 
k/2
(k-1)/2
Y
= 
*/
):
Y=
VG
= (a,
b). Vamos supor por absurdo e sem perda de generalidade que a